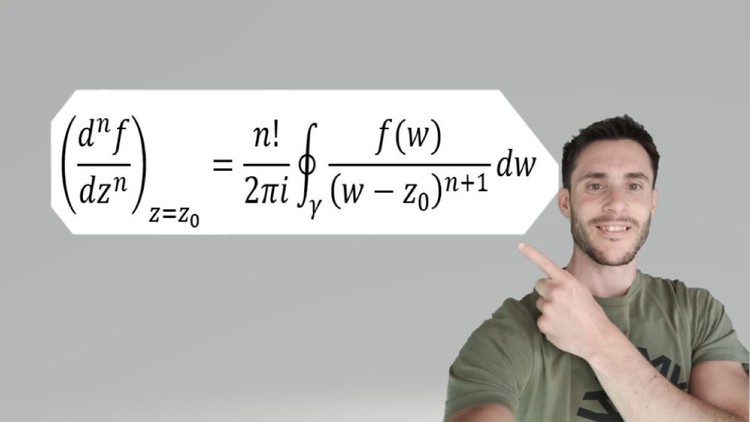Mastering Complex Calculus: From Derivatives to Residues

سرفصل های دوره

Complex Calculus: derivatives of complex variables, contour integration, Laurent series, Fourier series, and residues

1. Introduction to complex functions and derivatives of complex functions

1. functions of a complex variable part 1

2. functions of a complex variable part 2

3. Concept of derivative in complex calculus

2. Integration in Complex Calculus

1. integrals of complex functions and Cauchy theorem

2. Extension of Cauchy theorem

3. Cauchy integral formula part 1

4. Cauchy integral formula part 2

3. Laurent Series, Fourier Series, Taylor Series

1. Laurent series

2. Laurent series in compact form

3. Fourier series derivation from Laurent series

4. Fourier series generalization to any period T

5. Taylor series derivation from Laurent series

4. Residues and Contour Integration

1. Concept of Residue

2. Residue Theorem

3. Calculation of residues and coefficients of the Laurent series

4. Evaluation of a real integral using complex integration (exercise 1)

5. Contour integration to evaluate a real integral (exercise 2)

6. Contour integration to evaluate a real integral (exercise 3)

7. Another integral evaluated using the results of Complex Calculus (exercise 4)

8. Contour integration to evaluate a complex integral (exercise 5)

9. Another contour integration of a real integral - Exercise 6

10. Fresnel integral over the real line (formally derived with the residue theorem)

11. Hilbert transform and its geometric meaning

12. Solution to the diffusion equation using complex calculus and Laplace transform

13. Representation of the Dirac Delta

14. Abel-Plana formula in complex Calculus

15. Convolution of sinc functions using complex calculus

5. How residues aid in the interpretation of the Fourier Transform and its inverse

1. The importance of the Dirac Delta in defining the Inverse Fourier Transform

2. Another integral representation of the Dirac Delta

6. How to use complex calculus to attribute meaning to divergent series

1. Complex calculus to evaluate divergent series

2. Introduction to the analytic continuation of the Riemann zeta function

3. Train of impulses expanded in a Fourier series

4. Poisson summation formula

5. Application of Poisson summation formula

6. Another representation of the Riemann zeta function

7. Functional equation of the Riemann zeta function

8. Evaluation of the Riemann zeta function at s=-3

139,000 تومان

افزودن به سبد خرید

خرید دانلودی فوری

در این روش نیاز به افزودن محصول به سبد خرید و تکمیل اطلاعات نیست و شما پس از وارد کردن ایمیل خود و طی کردن مراحل پرداخت لینک های دریافت محصولات را در ایمیل خود دریافت خواهید کرد.

تولید کننده: Udemy-Training